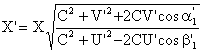НОВАЯ ТЕОРИЯ СТРОЕНИЯ АТОМОВ.

Г.И. Сухоруков, Э.Г. Сухоруков,  Р. Г. Сухоруков

Братск, Россия.

Бор и Зоммерфельд строго обосновали резерфордовскую планетарную модель атома [1,2]. Однако вследствие трудностей, возникших при объяснении тонкой структуры спектра атома водорода и строения сложных атомов, их теория была отвергнута. В настоящее время строение атомов описывается сложным трехмерным дифференциальным уравнением Шредингера [3-5]. Даже для атома водорода решение этого уравнения не удается выразить через элементарные функции [6]. Для атомов, имеющих два и более электронов, уравнение Шредингера не может быть решено даже численным образом [7]. Чтобы рассчитать спектральные термы одного сложного атома, требуется работа электронно-вычислительных машин в течении сотен часов [8] или нескольких лет [9].

Наша теория является логическим продолжением теории Бора-Зоммерфельда. При ее создании использовался обширный экспериментальный материал, связанный с определением значений ионизационных потенциалов и энергий термов оптических и рентгеновских лучей. В справочной литературе значения ионизационных потенциалов и энергий термов приводятся с очень высокой точностью, достигающей восьми - десяти значащих цифр. Эти данные надежны, так как получены в результате обобщения экспериментального материала, которым располагает все человечество. Результаты теоретических исследований, выполненных с использованием методик, разработанных на основе нашей теории, хорошо согласуются с вышеназванными экспериментальными данными.

Скорость распространения взаимодействия равна скорости света. Конечность этой скорости обусловлена наличием мировой среды (эфира). Законы Ньютона и Кулона точно выполняются только для тел, неподвижных относительно этой среды. Для движущихся тел эффективность взаимодействия зависит от скорости их движения относительно мировой среды. Формулы эффекта движения аналогичны формулам эффекта Доплера в оптике и акустике. Для случая, когда оба взаимодействующих тела движутся, формула имеет вид [10, 11]

,

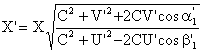где X � величина, зависящая от скорости движения, С � скорость света, V и U � скорости движения взаимодействующих тел, a₁ и b₁ - углы между направлениями движений источника и приемника волн и линией соединяющей точку, в которой волна излучилась, с точкой, в которой она встретилась с приемником. Буквами со штрихами и без штрихов обозначены величины, полученные соответственно с учетом и без учета эффекта движения. В атоме движением ядра можно пренебречь и тогда для величин, характеризующих движение электрода по круговой орбите можно записать

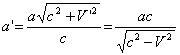,                                                (1)

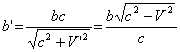,                                                (2)

где a и b � величины, значения которых соответственно увеличиваются или уменьшаются вследствие эффекта движения.

            Интеграл энергии системы электрон � ядро имеет вид [12]

,

где m � масса электрона, V� � скорость электрона, b = 1+ m/М, М � масса ядра, r� � радиус- вектор, m� = (z�e²c²10^-7)/m, z� � зарядовое число, e � элементарный заряд, l � длина большой оси орбиты. Определив с помощью интеграла энергии орбитальную скорость и ее радиальную и тангенсальную составляющие, можно вывести уравнение, описывающее движение электрона по финитной незамкнутой кривой [12]:

,

где j� � угол поворота радиуса-вектора r; n � число характеризующее степень вытянутости орбиты; k � номер стационарного состояния; V_a, V_n � скорости электрона в апоцентре и перицентре; r_a, r_n � апоцентральный и перицентральный радиусы.

            Результаты расчетов по формулам авторов с высокой точностью совпадают с экспериментальными данными. В таблице 1 приведены значения фундаментальных физических констант, полученных экспериментально и вычисленных по нижеприведенным формулам:

         ;            :                    :

         ;                  :             .

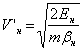Физические константы                                                                                 Таблица 1

            В качестве исходных данных взяты значения четырех констант [13]: скорость света с = 2,99792458×10⁸ м/с; элементарный заряд  e� = 1,60217733×10^-19 Кл; Масса электрона m = 9,10938968×10^{-31 кг; боровский радиус} r�_н = 5,29177249 10^{-11 м. Для атома водорода} b_н = 1,000544617.

            Параметры орбит сложных атомов можно выразить через параметры боровской орбиты [12].

Если электрон движется по круговой орбите,  то:

,                                                 (3)

а если по эллиптической, то:

;

,

где z� � эффективное зарядовое число,  - энсцентриситет.

Полная энергия системы электрон-атом:

.                                                         (4)

Период обращения электрона и ядра вокруг центра масс:

.                                                           (5)

С помощью формул (1) и (2) определены r_н = 0,529191323×10^{-10 м;}                      V_н = 2,186442460×10⁶ м/с; Е_н= 21,78571660×10^-19 Дж; e = 1,602156024×10^-19 Кл;   Т_н = 1,520657574×10^-16 с. Таким образом, зная эффективное зарядовое число, можно вычислить все величины, характеризующие движение электрона по орбите в атоме. 

            Атомы имеют планетарное строение. При переходе электрона из одного стационарного состояния в другое происходит поглощение или излучение волн. При этом в многоэлектронных атомах изменяется полная энергия не только у того электрона, который совершил переход с одной орбиты на другую, но и у всех остальных электронов. Длины оптических и рентгеновских волн, излучаемых сложными атомами, можно вычислить по формуле [12]

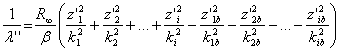,                       (6)

где  - зарядовые числа и стационарные состояния электронов у невозбужденного атома;  - соответствующие величины у возбужденного атома. Нумерация электронов идет в направлении от ядра к периферии атома. Постоянная Ридберга R_¥= 1,097314784×10⁷ м^-1 имеет одну и ту же величину у всех атомов.

Энергии спектральных термов атома водорода                                         Таблица 2

            В таблице 2  приведены значения термов атома водорода, взятые из справочника [14] и вычисленные по формуле (6). Расхождения между расчетными и справочными данными наблюдаются после пятой или шестой значащей цифры. Это объясняется тем, что последние цифры значений термов получены не экспериментально, а расчетом по ныне принятой методике. Разности же термов, характеризующих тонкую структуру спектров согласно существующей и новой теории совпадают точно.

            Параметры орбит многоэлектронных атомов можно рассчитать, используя значения ионизационных потенциалов. Расчет ведется в такой последовательности. Вначале по значениям ионизационных потенциалов [15] находятся приблизительные значения эффективных зарядовых чисел. Затем определяются кратности периодов обращения электронов по формулам:

            Выразив с помощью этих формул зарядовые числа всех электронов через зарядовое число наружного электрона и подставив новые выражения для зарядовых чисел в формулу (6), получим уравнение с одним неизвестным

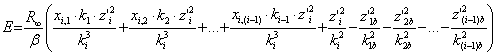.        (7)

Теперь можно определить точные значения  решая последовательно задачи для ионов данного атома, имеющих соответственно 2, 3, � , i электронов. Как показано выше, зная значение z� для электрона, можно определить все параметры его орбиты. В опубликованных работах приведены расчетные значения параметров орбит электронов у всех возможных ионов первых двенадцати элементов таблицы Менделеева. В данной статье приведен пример расчета атома гелия.

В невозбужденном атоме гелия оба электрона находятся в первом стационарном состоянии и движутся по круговым орбитам. Период обращения наружного электрона в два раза больше периода обращения внутреннего электрона. Чтобы удалить электрон из невозбужденного атома гелия, нужно затратить энергию Е=198310,76 Сн^-1 =  39,3933902×10^-19 Дж [14]. Для этого случая уравнение (7) примет вид:

.

Вычислив с помощью этого уравнения значения =1,3914422, из соотношения  = 2 найдем =1.9677965. Теперь по формулам (3), (4) и (5) можно вычислить параметры орбит обоих электронов, находящихся в первом стационарном состоянии.

Орбиты электронов в атоме гелия                                                            Таблица 3

В таблице 3 приведены вычисленные аналогичным образом зарядовые числа электронов в атоме гелия для случаев, когда наружный электрон находится в одном из трех стационарных состояний.

Как видно из таблицы 3, наружный электрон атома гелия в первом стационарном состоянии может иметь только одну круговую орбиту, во втором � 4 круговых и одну эллиптическую,  а в третьем � 5 круговых и две эллиптические. Первая орбита электрона во втором стационарном состоянии очень устойчива. Переход электрона с этой орбиты на орбиту в первом стационарном состоянии возможен только при соударении атомов [16]. Гелий обычно состоит из двух типов атомов. В одних атомах наружный электрон движется по орбите первого стационарного состояния, а в других по первой орбите второго стационарного состояния. Первые атомы являются атомами парагелия, а вторые атомами ортогелия.

Для ионов с одинаковым числом электронов, но разными зарядами ядер выполняется равенство:

где Е_н- ионизационный потенциал атома водорода, Е_n+1, Е_n и Е_n-1 -  ионизационные потенциалы ионов трех рядом расположенных элементов, n � порядковый номер элемента, k � номер стационарного состояния наружных элементов в ионах. По этой формуле вычислены ионизационные потенциалы и значения k у  24 элементов [12]. Никаких принципиальных трудностей нет для вычисления ионизационных потенциалов и параметров орбит электронов у всех элементов периодической системы.

Потенциалы ионизации атомов                                                                 Таблица 4

            В таблице 4 приведены расчетные и справочные значения ионизационных потенциалов у атомов фтора, неона и натрия. Как видим, расчетные значения ионизационных потенциалов хорошо согласуются со справочными.

            Химические и ряд физических свойств элементов обусловлены энергией связи наружных электронов с атомами. Энергия связи, а следовательно, и свойства имеют периодическую зависимость от порядкового номера элемента в таблице Менделеева. Если сравнить первые потенциалы ионизации у всех атомов [15], то можно четко выделить семь периодов, что и отражено в таблице Менделеева. Если же сравнить потенциалы ионизации у всех ионов с разными зарядами ядер, но с одинаковым количеством электронов, то также четко можно различить у известных нам элементов 12 периодов, которые приведены в таблице 5. В таблице приведен также 13-ый период для элементов, которые возможно существуют во Вселенной в условиях, отличных от условий Солнечной системы.

Периодический закон.                                                                                         Таблица 5

            В таблице 6 показано, как идет заполнение электронных слоев в атомах элементов 13-го периода, но по нему можно представить, как происходит заполнение электронных слоев в атомах всех остальных элементов. Число слоев в атоме соответствует номеру периода, в котором он находится. Максимально возможное число электронов в слое равно числу элементов в периоде, в котором заполняется этот слой. В первом слое оба электрона находятся в первом стационарном состоянии. Восемь электронов второго слоя находятся во втором, электроны третьего и четвертого слоя � в третьем, а электроны всех остальных слоев � в четвертом стационарном состоянии.

Распределение электронов в атомах 13 периода.                                       Таблица 6

            В уточненной периодической таблице элементов один период содержит два элемента, шесть периодов содержат по 8 элементов, четыре по 10 элементов, и два по 14 элементов. В некоторых периодах наблюдается одинаковая закономерность изменения свойств элементов по мере увеличения числа электронов во внешнем слое атома. Такие периоды будем называть подобными. Так подобными являются второй и третий периоды, начинающиеся с щелочных элементов; пятый, седьмой, десятый и тринадцатый, начинающиеся с элементов группы меди; четвертый, шестой, девятый и двенадцатый, содержащие по 10 элементов; восьмой и одиннадцатый, содержащие по 14 элементов.

 ЛИТЕРАТУРА

1.      Шпольский Э.В. Атомная физика. т.I � М.: Физмат, 1963.

2.      Зоммерфельд А. Строение атомов и спектры. т. I � М.: Гостехиздат, 1956.

3.      Вихман Э. Квантовая физика. т.4 � М.: Наука, 1986.

4.      Борн М. Атомная физика. � М.: Мир, 1967.

5.      Шпольский Э.В. Атомная физика т.2 � М.: Наука, 1984.

6.      Спролул Р. Современная физика. � М.: Фмзматгиз, 1961.

7.      Ландау Л.Д., Лифшиц Е.М. Квантовая механика. � М.: Физматгиз, 1961.

8.      Кравцов В.А. Массы атомов и энергии связи ядер. � М.: Атомиздат, 1974.

9.      Намбу Е. Кварки. � М.: Мир, 1984.

10.  Сухоруков В.И., Сухоруков Г.И. Эффект Доплера при движении источника и приемника волн в произвольном направлении // Акустический журнал. � 1986, т.32, №1. � с. 134-136.

11.  Сухоруков Г.И. Теоретические модели физического эксперимента. Диссертация на соискание ученой степени доктора физико-математических наук � Братск: 1998.

12.  Сухоруков Г.И., Сухоруков В.И., Сухоруков Р.Г. Реальный физический мир без парадоксов. � Иркутск: Изд-во иркут. ун-та, 1993.

13.  Власов А.Д., Мурин Б.П. Единицы физических величин в науке и технике: Справочние. � М.: Энергоатомиздат, 1990.

14.  Радциг А.А., Смирнов В.М. Справочник по атомной и молекулярной физике. � М.: Атомиздат, 1980.

15.  Таблицы физических величин. Справочник. Под ред. И.К. Кикоина. � М.: Атомиздат, 1976.

16.  Гольдин Л.П., Новиков Г.И. Введение в атомную физику. � М.: Наука, 1969.

 The Last renovation 08.10.2006
 � Site is created Kuimov O.S. at support ZAO "Hydrargium"