New Theory of Atomic Structure

Georgy Soukhorukov, Edouard Soukhorukov, Roman Soukhorukov

Bohr and Zommerfild definitely proved Rezerford�s planetary atomic model [1, 2]. However, as a result of difficulties appeared while explaining the fine atomic structure of hydrogen and complex atomic structure, their theory had been rejected. Now, atomic structure is described by the complex three-dimensional Shredinger�s differential equation [3..5]. Even for hydrogen atom, the solution of this equation cannot be expressed via elementary functions [6]. For atoms which have two or mode electons, Shredinger�s equation cannot be solved even by numerical way [7]. It takes electronic computers to work for hundreds of hours [8] or several years [9] to compute a spectrum therm.

Our theory is a logical continuation of Bohr and Zommerfield�s theory. An extensive material concerning the definition of values of the ionization potential and energy of therms of optical and x-rays had been used while formation. The referenced values of the ionization potential are given to high precision which reaches 8-10 decimal points.  These data are reliable because they are gotten as a result of summarizing of the experimental material which is available to all mankind. The results of the theoretical research conducted by using techniques developed on a basis of our theory are adjusted with the experimental data above.

The velocity of interaction propagation is equal to the velocity of light. The finiteness of this velocity is determined by presence of the universal medium (ether). Newton�s and Koulon�s laws are precisely applied only to solids which are static for this medium. For mobile solids, the effectiveness of interaction depends on the velocity of their motion relatively to the universal medium. The equations of the motion effect are similar to the equations of Doppler effect in acoustics and optics. In case that both of interacting solids are mobile, the equation takes following form [10, 11]:

where X is the value depending on the motion velocity, C is the velocity of light, V and U are velocities of motion on interacting solids, α₁ and β₁ are the angles between directions of motion of the wave source and the receiver and the line joining the point the wave emanated from with the point it met with the receiver. Accented and unaccented letters are given for the values obtained correspondingly taking and not taking into account the motion effect. The motion of atomic nucleus can be neglected, then, the following equations are possible for values characterizing the electron orbital motion:

;       ,                                    (1)

where a and b are the values which increase of decrease as a result of motion effect.

A velocity of an electron in the atom also depends on motion effect. It can be written as:

                                                                 .                                                             (2)

Having transformed the equation (2) to the following one

                                                                                                                                    (3)

we convince that

                                                            .                                                       (4)

During the calculation we have to use the values both considering and not considering the motion effect. Using equations (2) and (3) it is possible to switch from one values to another if one of velocity value - either V or V' � is known. Considering the equation (4) equations (1) can be written as:

                                                         ,                                                     (5)

                                                                                                             (6)

Atoms have planetary structure. When an electron turns from the one steady state to another, the waves are absorbed and emitted. At the same time, in the multi-electron atoms, not only the electron that moved from the one orbit to another, but also the rest of electrons have their full energy changed. The lengths of the optical and the roentgen waves emitted by the complex atoms are calculated according the formula [12]:

                                      ,                                  (7)

where:

β=1+, m is an electron mass, M is a kernel mass,

 are the charge counts and the steady states of a nonexcited atom, are the corresponding values of an exited atom. The electron numbering comes from the kernel to the periphery of the atom. Ridberg�s constant m^-1 is the same for all atoms.

The parameters of the orbits of an multi-electron atoms can be calculated via the values of the ionization potentials. Here is the sequence of calculations. First, the approximate values of an effective charge counts are calculated via the values of the ionization potentials [13]. Then, the repetition factors of the orbital periods are calculated by the following formulas:

These formulas help to express the charge counts of all electrons via the chare count of the external electron. Then, having put new expressions into the formula (8), we would have an equation with the one unknown value:

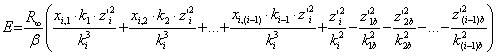                  .              (8)

Now it�s possible to determine the exact values  by sequential accomplishing the tasks for the ions of the given atom which have 2, 3, � , i electrons correspondingly. As it is shown above, having known the value z' for the electron, it is possible to determine all parameters of its orbit. In the published issues, the calculated values of the parameters of the electron�s orbits are given for all possible ions of the first twelve elements in the Periodic Table. In this article, the examples of calculation of the hydrogen and helium atoms are given.

Parameters of the orbit of complex atoms can be expressed through the parameters of Bohr orbit [12].

If an electron is moving on round orbit, then:

                                                             ,                                                         (9)

and if on elliptical, then

                                                 ;                                          (10)

                                                ,                                          (11)

                                                                                                                        (12)

where z' is an effective charge count, 

 is an eccentricity, where n is an orbital count, l and b are lengths of large and small axis of ellipse.

The full energy of an electron-atom system is:

                                                                     .                                                               (13)

The orbital period for the electron and the kernel to go around center of mass:

                                                                      .                                                                (14)

Formulas (1) and (2) have helped to determine: r_n = 0,529191323×10^{-10 m; V}_n = 2,186442460×10⁶ m/s; E_n = 21,78571660×10^-19 Joules; e = 1,602156024×10^-19 Coulomb; T_n = 1,520657574×10^-16 s.

Thus, having known the effective charge count it�s possible to calculate all magnitudes that characterize the electron�s orbital movement in the atom.

Table 1 shows the parameters of an electron�s orbit in the hydrogen atom for 4 steady states. Here�s the sequence of calculation. Equations (9 -11) have been used to calculate the velocities of an electron while moving on round and elliptical orbits. For the hydrogen atom these equations will look like (not considering the motion effect):

;  ;  .

The table shows real values of the velocity of an electron, i.e. considering the motion effect. These values have been calculated using the following equations:

;    ;    .

Effective charge counts for the electron which moves on round and elliptical orbits can be determined with the following equations:

,      .

The rest of parameters have been calculated using equations (12-14).

Table 1

Элементы орбит электрона в атоме водорода

Table 1 (continued)

Based on calculations conducted above it is possible to draw the following conclusions. Each orbit is characterized by only two quantum numbers which are k and n. In a hydrogen atom, charge count z is equal to 1 only for the electron which is static to the kernel. For the electrons which are moving on the orbit charge count z is more the 1. For the electrons which are in the same steady state but moving on the orbits with different values of n, lengths of a large axis are different so are the values of full energy. In a hydrogen atom, the parameters of the first Bohr orbit have been experimentally calculated at a very high precision. The parameters of the rest possible orbits can be calculated using equations above at a very high precision either.

In a nonexited atom of the helium, both electrons are in the first steady state and move on the round orbits. The orbital period of the external electron is twice more that the orbital period of the internal electron. Energy consumption to remove an electron from a nonexited helium atom is E� = 198310,76 Sn^-1 = 39.3933902�10^-19 Watt-Second. In this case, the equation (8) takes the following form:

.

Having calculated via this equation the values z^e₂ = 1.3914422, it is possible to find z'1 = 1.9677965 from  ratio. Now it is possible to calculate the parameters of the orbits of both electrons in the first steady state with the equations (9-14).

Table 2

Orbits of Electrons In The Helium Atom

Table 2 shows similarly calculated count charges of an electron in the helium atom for the cases when the external electron is in the one of three steady states.

Evidently from table 2, the external electron in the helium atom can have only one round orbit in the first steady state, 4 round and 1 elliptical in the second steady state, and 5 round and 2 elliptical orbits in the third steady state. The first orbit of the electron in the second steady state is very stable. Electron�s transfer from this orbit to the orbit in the first steady state is possible only when the atoms collide [15]. Usually, the helium consists of two kinds of atoms. In some atoms, the external electron is moving on the orbit of the first steady state, and on the first orbit of the second steady state in the others. The first atoms are the ones of the parahelium, and the second atoms are the ones of the orthohelium.

For the ions with the equal number of the electrons but different kernel charges, the following equity is valid:

where: En is the ionization potential of the hydrogen atom, En+1, En, and En-1 are the ionization potentials of the ions of three elements located next to one another, n is the number of the element, k is the number of the steady state of the external elements in the ions. By this formula, the ionization potentials and the values for k have been calculated for 24 elements [12]. There is no principal difficulties for calculating the ionization potentials and the parameters of the electron�s orbits for all elements in the Periodical Table.

Table 3

Atoms� Ionization Potentials

Table 3 shows the calculated and the referenced values of the ionization potentials of the fluorine, the neon, and the natruim atoms. Evidently, the calculated values of the ionization potentials conform well to the reference values.

Chemical and a set of physical properties of the elements are stipulated by the energy of binding external electrons with the atoms. The binding energy, and, therefore, the properties are periodically dependent on the number in the Periodical Table. While comparing the ionization potentials of all atoms [13] with the different kernel charges but with the equal number of the electrons, 12 periods shown in table 5 may be neatly discerned for known elements. Table also shows the 13^th period for the elements that possibly exist in the Universe in conditions different from ones in the Solar System.

Table 4

Periodical Law

Table 5 shows how the electron layers are filled in the atoms of the elements of the 13^th period. The period may give an idea how the electron layers are filled in the atoms of other elements.

The number of layers in the atom corresponds to the number of the period in which it is located. The maximum possible number of the electrons in the layer is equal to the number of elements in the period in which the layer is filled. In the first layer, both electrons are in the first steady state.

Eight electrons in the second layer are in the second steady state, the electrons of the third and the forth layer are in the third, and the electrons of all other layers are in the forth steady state.

Table 5

Electrons Allocation in the Atoms of 13^th Period

In a specified periodical table of elements one period contains two elements, six periods contain 8 elements each, four periods contain 10 elements each, and two periods contain 14 elements each. In some periods, there is the same regularity in the change of the element�s properties with the increase of the number of electrons in the atom�s external layer. Thus, the second and the third periods beginning with alkaline elements; the fifth, the seventh, the tenth, and the thirteenth periods beginning with the elements of the copper group; the fourth; the sixth, the ninth, and the twelfth containing 10 elements each; the eighth and the eleventh containing 14 elements each are similar.

The results of calculations on authors� equations concur to a high precision with the experimental data. Table 6 shows the values of fundamental physical constants obtained experimentally and calculated with equations below:

         ;            :                    :

         ;                  :             .

Table 6

Physical Constants

As a source data, the values of four constants have been taken [13]:

Velocity of Light c = 2.99792458×10⁸ mps;

Elementary Charge e' = 1.60217733×10^-19 Cl;

electron mass m = 9.10938968×10^-31_� kg;

Bohr radius r'n = 5.29177249×10^{-11 m.}

For hydrogen atom, b_n = 1.000544617.

Table 7

Energies of Spectral Therms of Hydrogen Atom

Table 7 shows the values of therms of a hydrogen atom taken from the reference [14] and calculated with the equation (7). The difference between the calculated and the referenced value appears after the fifth or sixth decimal point. This is because last digits of the therm values are given not experimentally, but calculated by the established principles. The differences of the therms characterizing the fine structure of spectrums according to existent and new theory are equal.

Bibliography:

1.      Шпольский Э.В. Атомная физика. т.I � М.: Физмат, 1963.

2.      Зоммерфельд А. Строение атомов и спектры. т. I � М.: Гостехиздат, 1956.

3.      Вихман Э. Квантовая физика. т.4 � М.: Наука, 1986.

4.      Борн М. Атомная физика. � М.: Мир, 1967.

5.      Шпольский Э.В. Атомная физика т.2 � М.: Наука, 1984.

6.      Спролул Р. Современная физика. � М.: Фмзматгиз, 1961.

7.      Ландау Л.Д., Лифшиц Е.М. Квантовая механика. � М.: Физматгиз, 1961.

8.      Кравцов В.А. Массы атомов и энергии связи ядер. � М.: Атомиздат, 1974.

9.      Намбу Е. Кварки. � М.: Мир, 1984.

10.  Сухоруков В.И., Сухоруков Г.И. Эффект Доплера при движении источника и приемника волн в произвольном направлении // Акустический журнал. � 1986, т.32, №1. � с. 134-136.

11.  Сухоруков Г.И. Теоретические модели физического эксперимента. Диссертация на соискание ученой степени доктора физико-математических наук � Братск: 1998.

12.  Сухоруков Г.И., Сухоруков В.И., Сухоруков Р.Г. Реальный физический мир без парадоксов. � Иркутск: Изд-во иркут. ун-та, 1993.

13.  Таблицы физических величин. Справочник. Под ред. И.К. Кикоина. � М.: Атомиздат, 1976.

14.  Радциг А.А., Смирнов В.М. Справочник по атомной и молекулярной физике. � М.: Атомиздат, 1980.

15.  Гольдин Л.П., Новиков Г.И. Введение в атомную физику. � М.: Наука, 1969.

16.  Власов А.Д., Мурин Б.П. Единицы физических величин в науке и технике: Справочние. � М.: Энергоатомиздат, 1990.

Information about authors:

Georgy I. Soukhorukov

42-A, Naymoushina Str., 8

Bratsk 665709

Russian Federation

Phone: +7 (3953) 37-9529 (home)

e-mail: nil_mu@brstu.ru

Edouard G. Soukhorukov

10, Studencheskaya Str., 802

Bratsk 665709

Russian Federation

Phone: +7 (3953) 37-9155

Roman G. Soukhorukov

53, Yubileynaya Str., 98

Bratsk 665730

Russian Federation

Phone: +7 (3953) 33-1803

Issue date: 22 August 2000

Electronic Version:

� Nauka I Tekhnika (Science And Technics)

www.n-t.org.

 The Last renovation 08.10.2006
 � Site is created Kuimov O.S. at support ZAO "Hydrargium"